
The results of the analysis were substantiated by plant tests. The control of particle size by water addition to the head tank can aggravate the circulating load variance and hence also increase the probability of “roping” the hydrocyclones. The results of the first two searches for optimal controller settings give the standard deviations of all controls and outputs of interest. Application of Theory to the Design of a Control Strategy for a Gold-Ore Milling Circuit U5 is the mass fraction of solids less than 75µm in the feed and K4 is the grinding rate constant. The pulp specific gravity was assumed to be constant. Where U4 is the mass flow of solids to the mill and W1 is the hold-up mass of solids. The contents of the mill were taken to be fully mixed and the mass fraction of solids less than 75µm in the mill was represented by X4 in an equation of the form The rod mill was of an overflow discharge type and thus it was assumed that the volume of pulp in the mill would be insensitive to changes in throughput. Where X1 is the mass of water in the mill and X2 is the mass of ore in the mill (excluding the grinding media of pebbles), K1, K2 and n are constants and σ is the specific gravity of the solids. It was postulated that the volume flow of pulp from the discharge of these mills could be represented by an equation of the form On-stream instrumentation measures mill motor currents, product particle size and percent solids, water flows to head tank and sump, levels in head tank and sump, volume flow of pulp to the head tank and density of pulp feeding one of the primary hydrocyclones. Pulp from the sump discharges to a head tank feeding two sets each of two hydrocyclones in series. It was considered a milling circuit, which comprises a rod mill and two pebble mills discharging into a common sump. The variance matrix of the system outputs is given byĭevelopment of a Model for a Gold-Ore Milling Circuit Where Ψ is the variance parameter matrix of the Wiener processes. The statistical steady state variance matrix Vx of the state variables is given by the solution of the Liapunov equation. Where Yt is the output vector and C is a constant matrix. The controller proportional bands and integral reset times will be imbedded in the elements of the matrix A. 1 can be expressed as a linear function of the state variables Measurable outputs of the system described by Eq. A is the system matrix and D is a matrix of disturbance influences. Where Xt is the state variable vector and Wt is a vector of Wiener processes which form the basis for modelling process disturbances. One approach to the problem of modelling dynamic systems subjected to random process disturbances is to postulate a priori that the system can be modeled by a finite set of linear, time invariant stochastic differential equations of the form

Linear Mill Models and Stochastic Control Theory Often, the response of the circuit to pulse or sinusoidal disturbances is used as a measure of the effectiveness of control. It is difficult to derive an objective measure of the effectiveness of any chosen control strategy. Ideally, mill circuits should be controlled so that excessive random disturbances are reduced in frequency and amplitude.
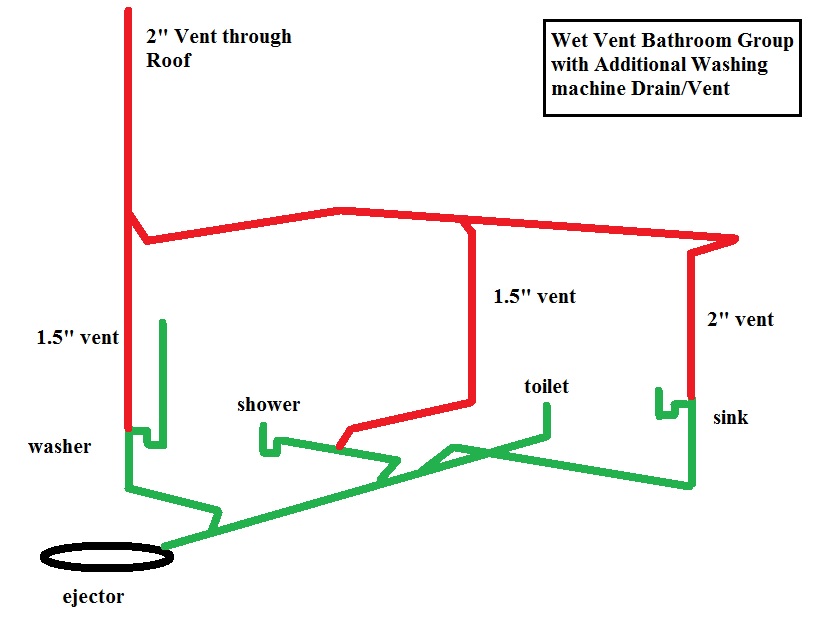
Linear Mill Models and Stochastic Control Theory.


 0 kommentar(er)
0 kommentar(er)
